
La teoria dell’informazione è un campo importante che ha dato un contributo significativo all’apprendimento profondo e all’IA, e tuttavia è sconosciuto a molti. La teoria dell’informazione può essere vista come una fusione sofisticata di elementi costitutivi fondamentali dell’apprendimento profondo: calcolo, probabilità e statistica. Alcuni esempi di concetti nell’intelligenza artificiale che provengono dalla teoria dell’informazione o dai campi correlati:
- Popolare funzione di perdita di entropia incrociata
- Costruire alberi decisionali sulla base del massimo guadagno di informazioni
- Algoritmo di Viterbi ampiamente usato in NLP e Speech
- Concetto di codificatore di encoder usato comunemente in RNN di traduzione automatica e vari altri tipi di modelli
Breve introduzione alla storia della teoria dell’informazione

All’inizio del 20 ° secolo, scienziati e ingegneri erano alle prese con la domanda: “Come quantificare l’informazione? Esiste un modo analitico o una misura matematica che ci può dire del contenuto informativo? “. Ad esempio, considera sotto due frasi:
- Bruno è un cane.
- Bruno è un grosso cane marrone.
Non è difficile dire che la seconda frase ci dà più informazioni in quanto dice anche che Bruno è “grande” e “marrone” oltre ad essere un “cane”. Come possiamo quantificare la differenza tra due frasi? Possiamo avere una misura matematica che ci dice quante più informazioni hanno la seconda frase rispetto alla prima?
Gli scienziati stavano lottando con queste domande. Semantica, dominio e forma di dati aggiunti solo alla complessità del problema. Quindi, il matematico e ingegnere Claude Shannon ha avuto l’idea di “Entropia” che ha cambiato il nostro mondo per sempre e ha segnato l’inizio di “Digital Information Age”.

Shannon ha proposto che “gli aspetti semantici dei dati sono irrilevanti”, e la natura e il significato dei dati non hanno importanza quando si tratta di contenuto informativo. Invece ha quantificato le informazioni in termini di distribuzione di probabilità e “incertezza”. Shannon ha anche introdotto il termine “bit”, che ha umilmente accreditato al suo collega John Tukey. Questa idea rivoluzionaria non solo gettò le basi della Teoria dell’informazione, ma aprì anche nuove strade per il progresso in campi come l’intelligenza artificiale.
Di seguito discutiamo di quattro concetti teorici di informazione popolare, ampiamente utilizzati e da conoscere in ambito di deep learning e data science:
entropia
Chiamato anche Entropia di informazioni o Entropia di Shannon.

Intuizione
L’entropia fornisce una misura di incertezza in un esperimento. Consideriamo due esperimenti:
- Lancia una moneta equa (P (H) = 0,5) e osserva la sua uscita, diciamo H
- Lancia una moneta parziale (P (H) = 0,99) e osserva la sua uscita, diciamo H
Se confrontiamo i due esperimenti, nell’esp 2 è più facile predire l’esito rispetto all’esp. 1. Quindi, possiamo dire che exp 1 è intrinsecamente più incerto / imprevedibile di exp 2. Questa incertezza nell’esperimento viene misurata usando l’entropia .
Pertanto, se c’è maggiore incertezza inerente nell’esperimento, allora ha un’entropia più alta. O meno l’esperimento è prevedibile, più è l’entropia. La distribuzione di probabilità dell’esperimento viene utilizzata per calcolare l’entropia.
Un esperimento deterministico, che è completamente prevedibile, diciamo che lanciare una moneta con P (H) = 1, ha entropia zero. Un esperimento che è completamente casuale, dice rolling fair dado, è meno prevedibile, ha massima incertezza e ha l’entropia più alta tra tali esperimenti.

Un altro modo di guardare l’entropia è l’informazione media acquisita quando osserviamo i risultati di un esperimento casuale. Le informazioni acquisite per un risultato di un esperimento sono definite come una funzione della probabilità di accadimento di quel risultato. Più il più raro è il risultato, più è l’informazione acquisita dall’osservarla.
Ad esempio, in un esperimento deterministico, conosciamo sempre il risultato, quindi nessuna nuova informazione acquisita è qui dall’osservazione del risultato e quindi l’entropia è zero.
Matematica
Per una variabile casuale discreta X , con possibili risultati (stati) x_1, …, x_n l’entropia, in unità di bit, è definita come:
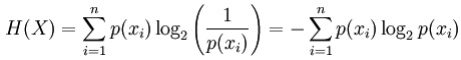
dove p (x_i) è la probabilità di I ^ esimo risultato di X .
Applicazione
- L’entropia viene utilizzata per la costruzione automatica di alberi decisionali. In ogni fase della costruzione di un albero, la selezione delle funzioni viene effettuata utilizzando i criteri di entropia.
- La selezione del modello basata sul principio dell’entropia massima, che stabilisce dai modelli in competizione uno con l’entropia più alta è il migliore.
Cross-Entropy
Intuizione
L’entropia trasversale viene utilizzata per confrontare due distribuzioni di probabilità. Ci dice quanto siano simili due distribuzioni.
Matematica
L’entropia incrociata tra due distribuzioni di probabilità p e q definite sullo stesso insieme di risultati è data da:
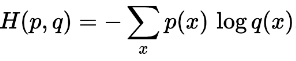
Applicazione
- La funzione di perdita di entropia incrociata è ampiamente utilizzata per i modelli di classificazione come la regressione logistica. La funzione di perdita di entropia incrociata aumenta man mano che le previsioni divergono dalle uscite reali.
- Nelle architetture di apprendimento profondo come le reti neurali convoluzionali, lo strato finale di “softmax” utilizza frequentemente una funzione di perdita di entropia incrociata.
Informazioni reciproche
Intuizione
L’informazione reciproca è una misura della dipendenza reciproca tra due distribuzioni di probabilità o variabili casuali. Ci dice quante informazioni su una variabile sono trasportate dall’altra variabile.
L’informazione reciproca cattura la dipendenza tra variabili casuali ed è più generalizzata del coefficiente di correlazione della vaniglia, che cattura solo la relazione lineare.
Matematica
Le informazioni mutue di due variabili casuali discrete X e Y sono definite come:
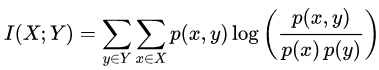
dove p (x, y) è la distribuzione di probabilità congiunta di X e Y , e p (x) e p (y)sono la distribuzione di probabilità marginale di X e Y rispettivamente.
Applicazione
- Selezione delle funzionalità: anziché utilizzare la correlazione, è possibile utilizzare le informazioni reciproche. La correlazione acquisisce solo le dipendenze lineari e perde le dipendenze non lineari ma le informazioni reciproche no. L’indipendenza reciproca di zero garantisce che le variabili casuali siano indipendenti, ma la correlazione zero no.
- Nelle reti bayesiane, l’informazione reciproca viene utilizzata per apprendere la struttura delle relazioni tra variabili casuali e definire la forza di queste relazioni.
Kullback Leibler (KL) Divergenza
Chiamato anche Entropia relativa.

Intuizione
La divergenza di KL è un’altra misura per trovare somiglianze tra due distribuzioni di probabilità. Misura quanto una distribuzione diverge dall’altra.
Supponiamo, abbiamo alcuni dati e una vera distribuzione sottostante è “P”. Ma non conosciamo questa ‘P’, quindi scegliamo una nuova distribuzione ‘Q’ per approssimare questi dati. Dato che “Q” è solo un’approssimazione, non sarà in grado di approssimare i dati come “P” e si verificherà una perdita di informazioni. Questa perdita di informazioni è data dalla divergenza di KL.
La divergenza KL tra ‘P’ e ‘Q’ ci dice quante informazioni perdiamo quando proviamo ad approssimare i dati dati da ‘P’ con ‘Q’.
Matematica
La divergenza KL di una distribuzione di probabilità Q da un’altra distribuzione di probabilità P è definita come:
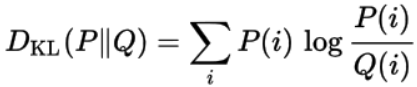
Applicazione
La divergenza KL è comunemente usata in autoincodenziatori a variazione continua non presidiata.
Information Theory è stato originariamente formulato dal matematico e ingegnere elettrico Claude Shannon nel suo seminario “A Mathematical Theory of Communication” nel 1948.
Nota: gli esperimenti sui termini, la variabile casuale e l’intelligenza artificiale, l’apprendimento automatico, l’apprendimento approfondito, la scienza dei dati sono stati usati in modo approssimativo ma hanno significati tecnicamente diversi.
Se ti è piaciuto l’articolo, seguimi Abhishek Parbhakar per altri articoli relativi a AI, filosofia ed economia.
